Table of contents
- How Do Computers Read Program
- What is Bit Manipulation
- Bitwise Operators
- Truth Table of Bit Operators
- Binary Number System
- Conversion of Decimal Numbers to Binary
- Conversion of Binary Numbers to Decimal
- Solving Problems Using Bitwise Operator
- A Simple C Program to Solve Problems
- Creating a Calculator For Bitwise Operation Using C Programming
- Conclusion
How Do Computers Read Program
Programming Languages are typically translated into machine codes, which are represented in binary (0s and 1s) and can be directly executed by the computer.
While you are writing programs in human-readable form, it goes through a compilation or interpretation process. This is where it converts it into a computer-readable form (Machine Codes which are represented in binary 0s and 1s). 0 typically signifies OFF or False while 1 signifies ON or True.
What is Bit Manipulation
Bit Manipulation can be seen as switches in a house that are connected to different bulbs. The process of turning ON and OFF the bulbs through the switch is called Bit Manipulation.
Bit Manipulation refers to the process of manipulating individual bits of a byte within binary data using bitwise operations. It involves performing operations at the bit level to extract, modify, or combine specific bits of data.
in a byte, there are 8 bits. The process of manipulating the bits is called Bit Manipulation. Of all other programming languages, C and C++ has special features to manipulate an individual bit of a byte. This feature is implemented by using bitwise operators that support bitwise operation.
Bitwise Operators
Bitwise operators are operators that perform operations on individual bits within a binary representation of numbers. They allow programmers to manipulate the binary value of operations at the bit level.
| OPERATORS | DESCRIPTION | |
| Bitwise AND (&) | Copies a bit to the result if it exists in both operands | |
| Bitwise OR ( | ) | Copies a bit to the result if it exists in either operands |
| Bitwise Exclusive OR (^) | Copies a bit if it is set in one operand but not both | |
| One's Complement (~) | It is a unary operator which has the effect of flipping bits (a unary operator is an operator that operates in a single operand). | |
| Bitwise Left Shift (<<) | The left operand value is moved left by the number of bits specified by the right operand | |
| Bitwise Right Shift (>>) | The left operand value is moved right by the number of bits specified by the right operand |
Truth Table of Bit Operators
| P | Q | P & Q | P | Q | P ^ Q | ~P | ~Q |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Binary Number System
The Binary Number System also known as the base-2 system is a numeral system that uses only two digits 0 and 1. The more familiar number system widely known and most used is the Decimal System (base-10) uses digits from 0-9 and represents numbers using a power of 10. In binary, each digit is called a bit.
Binary Numbers are widely used in computer systems and digital electronics because they can directly represent the ON/OFF state of the electronic component.
Understanding the Binary Number System is crucial for tasks such as Bitwise Operation.
Conversion of Decimal Numbers to Binary
Here are the steps to convert a Decimal number to a Binary
Start with the decimal you want to convert.
Divide the decimal number by 2 (the base of the binary system).
Write down the remainder (either 0 or 1).
Divide the quotient obtained in the previous step by 2 again
Write down the remainder
Repeat steps 4 and 5 until the quotient becomes 0
Write down the remainder obtained in reverse order. This will give you the binary representation.
For example:
Let's convert 100 and 30 using the steps above
To convert 100 to base-2
| 2 | 100 |
| 2 | 50 rem 0 |
| 2 | 25 rem 0 |
| 2 | 12 rem 1 |
| 2 | 6 rem 0 |
| 2 | 3 rem 0 |
| 2 | 1 rem 1 |
| 0 rem 1 |
The final answer in reverse order is = 110 0100 which can also be written as 0110 0100
To convert 30 to base-2
| 2 | 30 |
| 2 | 15 rem 0 |
| 2 | 7 rem 1 |
| 2 | 3 rem 1 |
| 2 | 1 rem 1 |
| 0 rem 1 |
The final answer in reverse order is = 1 1110 which can also be written as 0001 1110
Conversion of Binary Numbers to Decimal
Here are the steps to convert a Binary number to a Decimal
Start with the binary number you want to convert.
Using a super-script, identify the position (from right to left) of each digit in the binary number starting with position 0.
Assign powers of 2 to each position, starting from 2^0 for the rightmost digit, 2^1 for the next digit, 2^2 for the next, and so on.
Multiply each binary digit by its corresponding power of 2.
Sum up the result of the multiplication.
Here's an example:
To reconvert 0110 0100 to base-2
70615140 30211000 2 = 0 * 27 + 1 * 26 + 1 * 25 + 0 * 24 +0 * 23 + 1 * 22 + 0 * 21 + 0 * 20
70615140 30211000 2 = 0 + 64 + 32 + 0 + 0 + 4 + 0 + 0
70615140 30211000 2 = 100
i.e 0110 0100 = 100 in base 10
To reconvert 0001 1110 to base-10
70605041 31211100 2 = 0 * 27 + 0 * 26 + 0 * 25 + 1 * 24 +1 * 23 + 1 * 22 + 1 * 21 + 0 * 20
70605041 31211100 2 = 0 + 0 + 0 + 16 + 8 + 4 + 2
70605041 31211100 2 = 30
i.e 0001 1110 = 30 in base-10
Solving Problems Using Bitwise Operator
Using the Bitwise Operators to Solve a Problem
100 and 30 as a case study.
| Bitwise AND | |
| 0110 0100 | (100 converted to base-2) |
| & (AND) | |
| 0001 1110 | (30 converted to base-2) |
| 0000 0100 | (When converted to base-10, the answer will be 4.) |
| Bitwise OR | ||
| 0110 0100 | (100 converted to base-2) | |
| (OR) | ||
| 0001 1110 | (30 converted to base-2) | |
| 0111 1110 | (When converted to base-10, the answer will be 126.) |
Bitwise XOR | |
0110 0100 | (100 converted to base-2) |
^ (XOR) | |
0001 1110 | (30 converted to base-2) |
0111 1010 | (When converted to base-10, the answer will be 122.) |
One's Complement | |
0110 0100 | (100 converted to base-2) |
~ (flips the bit from 0-1 and 1-0.) | |
1001 1011 | (When converted to base-10, the answer will be -101.) |
| Left shift | |
| 0001 1110 | (30 converted to base-2) |
| <<2 (shifts the bits in 2's from the left and add 0 from the right) | |
| 0111 1000 | (When converted to base-10, the answer will be 120.) |
| Right shift | |
| 0110 0100 | 100 converted to base-2 |
| \>> 2 (shifts the bits in 2's from the right and add 0 from the left) | |
| 0001 1001 | (When converted to base-10, the answer will be 25.) |
A Simple C Program to Solve Problems
#include <stdio.h>
int main()
{
unsigned int a, b;
a = 100; /* 100 = 0110 0100*/
b = 30; /* 30 = 0001 1110*/
int result;
result = a & b;
/*
* converts both operands to base-2 and solve.
* After solving with AND operation, it reconverts it to base-10
* The final answer will be = 4
*/
printf("The Bitwise AND of %u and %u is: %d\n", a, b, result);
result = a | b;
/*
* converts both operands to base-2 and solve.
* After solving with OR operation, it reconverts it to base-10.
* The final answer will be = 126
*/
printf("The Bitwise OR of %u and %u is: %d\n", a, b, result);
result = a ^ b;
/*
* converts both operands to base-2 and solve.
* After solving with XOR operation, it reconverts it to base-10.
* The final answer will be = 122
*/
printf("The Bitwise XOR of %u and %u is: %d\n", a, b, result);
result = ~a;
/*
* converts the operand to base-2.
* flip the bit i.e. from 0 to 1 and 1 to 0,
* it reconverts it to base-10.
* The final answer will be = -101
*/
printf("The One Complement of %u is: %d\n", a, result);
result = ~b;
/*
* converts the operand to base-2.
* flip the bit i.e. from 0 to 1 and 1 to 0,
* it reconverts it to base-10.
* The final answer will be = -31
*/
printf("The One Complement of %u is: %d\n", b, result);
result = a >> 2;
/*
* converts the operand to base-2.
* right shift the bits in two's i.e 0110 0100 will be 0001 1001,
* and it reconverts it to base-10.
* The final answer will be = 25
*/
printf("The Bitwise Right Shift of %u is: %d\n", a, result);
result = b << 2;
/*
* converts the operand to base-2.
* left shift the bits in two's i.e 0001 1110 will be 0111 1000,
* it reconverts it to base-10.
* The final answer will be = 120
*/
printf("The Bitwise Left Shift of %u is: %d\n", b, result);
return 0;
}
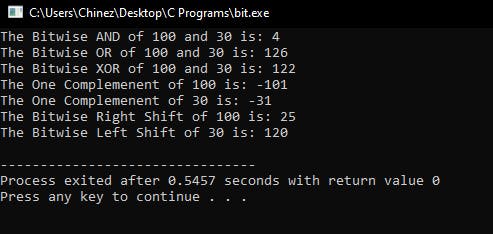
This is the Final Output
Creating a Calculator For Bitwise Operation Using C Programming
#include <stdio.h>
#include <stdlib.h>
/**
* main- Entry point of the program
*
* Description:
* This program allows the user to perform various bitwise operations on two
* numbers or perform bitwise shifting and complement operations on a single number.
* The user is prompted to choose an operation and provide the necessary inputs.
* The result of the operation is then displayed.
*
* Return: 0 on successful execution
*
*/
int main()
{
unsigned int firstNumber; //First number input by the user
unsigned int secondNumber; //Second number input by the user
int result; // Variable to store the result of the bitwise operation
int Operator; // User choice of bitwise operator
int shift; // Number of positions to shift in case of left or right shift
printf("Enter two numbers and a number where required!\n");
do {
printf("Choose a Bitwise Operator\n");
printf("1. Bitwise AND\n");
printf("2. Bitwise OR\n");
printf("3. Bitwise XOR\n");
printf("4. One's Complement\n");
printf("5. Bitwise Left Shift\n");
printf("6. Bitwise Right Shift\n");
printf("0. Exit\n");
printf("Enter your chioce of Bitwise Operator: ");
scanf("%d", &Operator);
if (Operator == 1){
printf("Enter the first number\n");
scanf("%u", &firstNumber);
printf("Enter the second number\n");
scanf("%u", &secondNumber);
result = firstNumber & secondNumber;
printf("The Bitwise AND for %u and %u is %d", firstNumber, secondNumber, result);
}
else if (Operator == 2){
printf("Enter the first number\n");
scanf("%u", &firstNumber);
printf("Enter the second number\n");
scanf("%u", &secondNumber);
result = firstNumber | secondNumber;
printf("The Bitwise OR for %u and %u is: %d", firstNumber, secondNumber, result);
}
else if (Operator == 3){
printf("Enter the first number\n");
scanf("%u", &firstNumber);
printf("Enter the second number\n");
scanf("%u", &secondNumber);
result = firstNumber ^ secondNumber;
printf("The Bitwise XOR for %u and %u is: %d", firstNumber, secondNumber, result);
}
else if (Operator == 4){
printf("Enter a number\n");
scanf("%u", &firstNumber);
result = ~firstNumber;
printf("The One's complement for %u is: %d", firstNumber, result);
}
else if (Operator == 5){
printf("Enter a number\n");
scanf("%u", &firstNumber);
printf("What position do you want to left shift to?\n");
scanf("%d", &shift);
result = firstNumber << shift;
printf("The One's complement for %u is: %d", firstNumber, result);
}
else if (Operator == 6){
printf("Enter a number\n");
scanf("%u", &firstNumber);
printf("What position do you want to Right shift to?\n");
scanf("%d", &shift);
result = firstNumber >> shift;
printf("The One's complement for %u is: %d", firstNumber, result);
}
else if (Operator == 0) {
printf("Exiting the program. Goodbye and have a nice day!\n");
}
else {
printf("Error, wrong input.");
}
printf("\n \n");
}
while (Operator != 0);
return 0;
}
You can test and run the program to see the output.
Conclusion
Bit manipulation requires careful handling and understanding of binary representation as well as consideration for platform-specific behaviour and byte order. it is important to ensure code clarity and readability when working with bitwise operations by providing appropriate comments and using meaningful variable names.
That's it for today, folks.
You can follow me on Twitter and also on LinkedIn for more...


